The Ancients Used Gods
Alyn Rockwood
 |
One Two objects occupy different space and have separate outward appearances, but a very similar creation process. |
Treading into art as a scientist
“The ancients used gods to organize the universe. In modern times we use ‘cause and effect’ [science], not that it is the truest, but only more convenient.” -Henri Poincare.
Poincare’s quote would be clear heresy in the world of science, except that Poincare was indisputably one of the world’s greatest mathematicians; his words demand consideration based on nothing else than his prodigious achievements. In order to do that one needs to put his words in context, and that means one needs to think like a mathematician. It will surprise many to discover that “thinking like a mathematician” means thinking a lot like an artist. In fact, it is not uncommon to encounter mathematicians who prefer to describe themselves as artists, rather than scientists.
The gods who have gained popularity in our day are organized and purposeful with pretty well defined dogma. In contrast, the gods of the ancients were capricious,inscrutable and mysterious. Using them to organize the universe left one with a sense of mystery, as well as insecurity. The mathematicians, to whom I include the great research scientists, not only live with ambiguity, but they embrace it willingly. It is the rich, dark soil from which ideas spring. Ambiguity motivates them to seek out new answers. Without ambiguity science would be fat and indolent.
I recall as a young boy actually feeling pain because I could not figure out how the spinning of the earth and its revolution around the sun were so coordinated as to keep from flinging me into space. I since learned about gravity, and although I can now characterize it mathematically and compute the force between masses I am still no closer to really understanding how it works. At least, I worry less about being flung into outer darkness.
Gravity has an interesting legacy in science. Newton spent years considering gravity. He was soon frustrated considering a theory that some sort of string connected everything.The likely apocryphal story of him under the apple tree had its origins in that he did return to his family farm when Cambridge was closed because of the plague. During this time he became interested in Hermeticism, which formed the philosophical basis for alchemy. Newton was for a time a serious student of alchemy. Its emphasis on categorizing the universe into repellers and attractors gave him the right mindset to approach gravity in a fresh way, so that when he returned to Cambridge he produced the results we use today. Who is to say that Hermeticism and alchemy were not the “truest”way to think for Newton? Better than some string theory?
Newton, armed with his new view about masses attracting each other, quickly derived the gravitation formula from Kepler’s laws that described the orbits of the planets. Keller these only because he had accepted Galileo’s rejection of an earth-centered universe. They all trod into uncertain realms of knowledge; and they might well have been wrong, in which case we would not know their names.
In this short description the parallels to the great artists of that period should be apparent. Einstein punctuates this idea for us:
The fairest thing we can experience is the mysterious. It is the fundamental emotion,which stands at the cradle of true art and true science. He who knows it not and can no longer wonder, no longer feels amazement, is as good as dead, a snuffed-out candle.
-Albert Einstein
Ambiguity and mystery constitute one similarity between artists and mathematicians .Another set of similarities is found in the in the execution of their ideas.
Consider a work by the artist Jasper Johns:
0 through 9, 1961.
Open this link to the work on the Metropolitan Museum site
If you stare at the long enough, you will eventually see all the digits from 0 to 9. Furthermore, you will also recognize bearded man embedded within the numbers -- perhaps a great mathematician?
The first question: - where did Johns get the idea to do this? All artists have that moment where they stare at a blank canvas, or uncut stone. There is that instant where the first stroke is laid down. Mathematics presents the same experience. The first step in mathematics, a sketch of geometry, or a rigorous statement of the problem is a blank piece of canvas. When the first line of symbols emanates from the pen, it is as creative for the mathematician as the first stroke from the artist – and just as important.
Secondly, imagine the challenge facing Johns to make his drawing work. Undoubtedly lines had to be shifted, some darkened, erasures, redraws, filling in negative space. It is an exercise to manipulate the pieces with respect to each other, while constantly driving towards the goal. This is so much like mathematics. How shall an expression be manipulated, how do the linear elements work with each other, and what manipulations can bring me closer to my goal?
The Johns example captures the operational similarities; it is the natural thing for a scientist to see when looking at art to look at implementation. This and the love of the mysterious are salient similarities from the scientists view. Next we consider the medium.
Mathematics is Literature
“Poetry is a science as precise as geometry.” -Flaubert
“Geometry is an art as sublime as poetry.” -Rockwood
Mathematics is a literary form. Development of the literary style in mathematics had as much to do with its progress as the invention of new methods of calculation.
The equation is, as we have all experienced in high school, a fundamental part of mathspeak. It is a complete sentence with noun, verbs (:equals”, “plus”, “,multiply” etc.) and objects (numbers variables etc.) There is a well defined, but rich set of rules for manipulating the sentence. Recall your high school teacher saying, “you can divide both sides of the equation with the same quantity as long as it is not zero.” The equation is musical theme; its manipulations are variations on the theme. The resulting variations
give us new insights into the original theme. If we string enough of them together and achieve significant new insight it is one way to create what we call a theorem, i.e., we “prove” a theorem.
The equation is not the only grammatical device in mathematics, far from it, but it is an important one,and it will serve as a good example to illustrate the language development of mathematics.
Consider the economy and power of a phrase like x2 + y2 + (x + y)1/2 compared with the Babylonian equivalent, which was used inland surveying.
Good mathematical style conveys not only the meaning of the language, but also suggests how to perform the calculations. This allows even the layperson to compute 23 times 58, for example. Pity the poor Roman who had to figure out XXIII times LVIII. The Roman representation does not suggest how to do it. It was no wonder that mathematicians of the time, who could compute land area or even multiply two numbers together, were highly treasured professionals, commanding large salaries (sigh). In modern digital parlance we would say Arabic numerals constitute a good user interface.So it is with any good mathematics.
The Greeks, for all their advancement in mathematics, faced one enormous problem.They believed that the only “true” numbers were integers, or ratios of integers, i.e. fractions. This limited their ability to accept π, for instance; or more importantly solve simple equation like
x2 = 2. Greeks had developed considerable expertise in solving equations with integer solutions,but they had difficulty moving beyond their religious belief about numbers. The word irrational comes from a number not being a ratio. We now apply it to faulty thinking because Greeks felt that way about numbers like √2 = 1.4148…, which cannot be written as a ratio of integers. Being unable to solve such simple equations severely inhibited development of their mathematical language. Imagine, say, a religious belief that disallowed the use of pronouns in a sentence. How would that have affected literature? The Greeks belief had much weightier consequences for mathematics. In this case their gods had organized the universe inconveniently. . Ironically, it was a Greek, one of followers of Pythagoras, named Hipposas, who first proved that √2 was not a rational number. The idea was so abhorrent to Pythagoras that, according to one version, he had poor Hipposas executed. It took almost 2000 year sand a Renaissance before mathematicians began to accept Hipposas’ idea, and that equations like x2 = 2 had solutions that were “real” numbers, not rational. There was a sudden explosion in mathematical thinking.
A very important development for digital arts came when it was realized by Descartes that geometric shapes could be represented by algebraic equations. Even today we actively pursue novel ways to represent shapes as equations, which the computer can save and render. See the image below, Bronze Age, which is a simple two-line equation.
 |
“Bronze Age,” a complex shape, simple equation. Alyn Rockwood ©2008 |
As with Hipposas before them, a group of Italian mathematicians (del Ferro, TartagliaBombelli) began studying a simple question – what if x2 = -1 had a solution? We know that no “real” number works. Descartes, exhibiting the religious zeal of the earlier Greeks, derisively called their work “imaginary.” It stuck. The imaginary number i was designated to solve the equation, that is, i2 = 1. The Italians and several generations of famous mathematicians following them generated an entire algebra of these numbers with a new addition, subtraction, multiplication and division etc. It was consistent and elegant. It was a beautiful piece of poetry, and of course, it had no practical application, it was, after all, imaginary. Gotta love those Italians!
Several hundred years later, we now regard complex numbers as so valuable in real world applications from electric circuits to quantum mechanics that it is studied under the general category of “applied” math, leading the famous computer scientist Richard Hamming to state “God made the universe with complex numbers.” How could those Italians have been so prophetic with their simple question?
Examples such as this have developed a belief system in mathematics that the most valued quality in good mathematics is elegance. Elegant mathematics delivers new idea sand experience with eloquent language. It opens up new worlds of thought with poetic experience. Without that internal beauty, the mathematics won’t stand the test of time.This is the mathematical mantra, and the history seems to bear it out. It is what Nobel physicist Eugene Wigner called “the unreasonable effectiveness of mathematics.”
See: http://www.dartmouth.edu/~matc/MathDrama/reading/Wigner.html
If you consider that mathematics is just a string of symbols put together with certain syntactical rules, and yet it embeds such deep concepts as quantum theory or relativity, it is pretty amazing. Why do we say these symbols represent reality? It is because they really work, for the most part, not because they are true. It is a wonder.
Just when we thought that the book on numbers was finished, Georg Cantor was to write yet another important chapter at the end of the 19th century. His thinking was fresh and innovative and the results were stunning, even to the sophisticated world of mathematic sat the time. Among the results he proved was that rational numbers are countable. That means you can associate every fraction with one and only one integer. How can that be? I can name a million fractions between 0 and 1, namely 1/1,000,000. 2/,1,000,000 … and so forth. (I could do a trillion too). Still, Cantor not only proved it, but also showed accounting scheme to actually make it happen. Then he showed that the rational, appeared far less frequently than the irrationals, that is numbers like √2 and π, of which I can only name a handful, were more common than the trillion fractions I can name. In fact, if I pick a real number at random the probability of getting a fraction is zero! That’s how many irrationals there are. If this boggles your mind, it turned mathematicians of the day vitriolic. No less a luminary than Poincare himself would call Cantorism a “ grave disease“, and he used all of his considerable influence to see that Cantor would not get published. Another prominent mathematician, Kronecker, called Cantor “a corrupter of youth.” Cantor was ultimately committed to an asylum, some say as a result of the ostracism and verbal assaults. Moving the culture and language of mathematics can be serious and dangerous business as with any art.
Unfortunately, the language of mathematics became so specialized and arcane that it created a divide between those who can read it and those who don’t. It is a divide that belies the thought processes that both mathematicians and artists have so much in common, and it can hide the splendor of its literature.
Treading into Math as an Artist
We again refer to Descartes’ discovery that geometric shapes could be represented by algebraic equations. My artist friends tell me it is still difficult for artists to believe that algebra generates the art of, say, a
Helaman Fergusonhttp://www.helasculpt.com or
a Bathsheba Grossman http://www.bathsheba.com/math
I am therefore going to give an example. No math background is really needed, in spite of the equations!
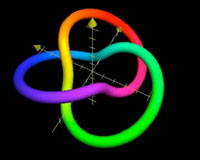
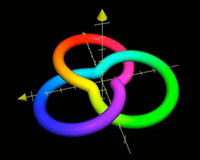
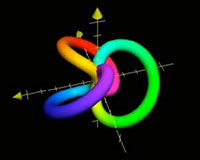
When R=2, k=1, p=2 and q=3, I produced my desired object the Trefoil knot (below). Knowing that the sine and cosine functions (sin, cos) would give me the right sort of twisting that Needed is a matter of mathematical experience. It is much like a painter knowing how pigments will mix. Moreover, different values of k would flatten my knot such as k=1/4 in the image of the knot flattened. Different values of R expanded and contracted my knot such as R=1 in the knot contracted.
 |
 |
 |
the Trefoil knot |
the knot flattened |
he knot contracted |
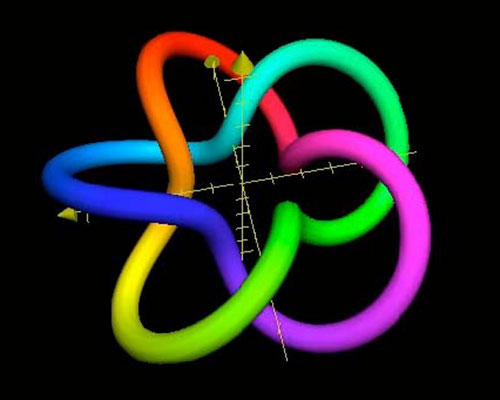 |
The 3-5 Torus Knot Choosing these numbers was an aesthetic decision and takes some skill with a good eye. There is also artistic serendipity similar to color bleeding in painting. |
Once I had the equations in front of me I could play around with my “ p’s and q’s.” I got other knots like those in the 3-5 Torus Knot and the 3-4 Torus Knot. Wow! In 1986 I finally submitted and had something like the 3-5 Torus Knot accepted to the SIGRAPH Art Show.
By the way, this is a case where my p’s and q’s need to be integers – maybe they are the “true” numbers, after all, at least for the gods of knot theory.
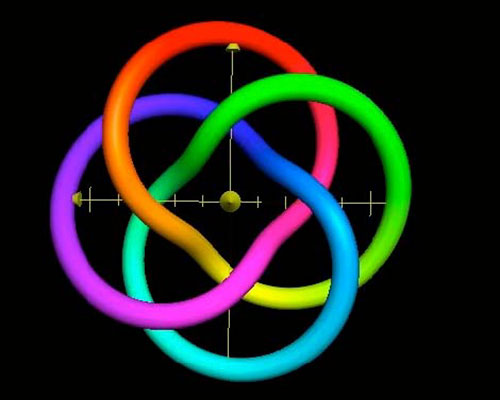 |
The knot hung around in my consciousness. In 1998 I suggested a version of it as the basis for the SIGGRAPH99 conference logo. |
The knot formula can be demystified a bit. The mental image I held, which led me to the equations, was that of wrapping a string around a donut. It would go around through the hole p times for every q revolutions before tying it off. Elegant, eh?
With these tools, I take the knot in the 3-5 torus knot (see above) replicate it, rescale the replication, change the sizes, colors and reposition the two together (as Johns); eventually ending up with the image at the top of the page of two objects occupying different space, the thematic image for this article. It is called “One.”
Finally, I should note that everything in math gets re-invented at one time or the other. All this stuff had been well-known to the knot-theorists (yes, they exist and have developed an extensive science. Do a wiki on knot theory!). However, I got to bring it to computer graphics and have my own personal and creative moment with it.
Conclusion
It is appropriate to have this brief discussion about art and mathematics in the Digital Arts Review. The computer has created a dramatic new medium whereby mathematics and art can enhance each other as never before. The mathematical underpinnings for a program like Photoshop or MAYA are considerable, for instances, but for the most part hidden from the artist who makes beautiful images and animations from them.
It is intriguing to contemplate the future of this relationship. No doubt mathematics will continue to improve both the modeling and rendering abilities of the artist and animator. The current tools are, at best, second generation. Digital technology, correctly coupled with the right mathematical algorithms, will eventually become the preferred media for the artist, from laying down oil glazes and brush strokes to creating bronzes or making full-length movies. It will not replace the artistic thinker, just the drudgery of dealing with the media. In fact, the artist’s skills will be in greater demand to create the content for the new techniques.
Furthermore, there will be an explosion of mathematical art as the artist will find it much easier to explore a domain, once exclusive to a few, who spoke the language. Consider the effect mathematical perspective had in art. There will be much more to come. I tried to represent this in the thematic image in at the top of the page. While one may have a preconceived notion about which object represents art and which one math; it may be the other way round, and maybe it doesn’t matter?
I have examined the kinship between art and math by (1) looking at art as a scientist, (2) looking at math as language with its own style, and (3) looking at math as an artist.
Religion
“An intelligent observer seeing mathematicians atwork and listening to them talk might conclude that they are devotees of exotic sects, pursuers of esoteric keys to the universe.”
-Davis and Hersch, The Mathematical Experience
I don’t need to say much about the religious fervor of artists; it is well known.
With respect to mathematics, at one end of the religious spectrum is a view epitomized by Physicist Max Tegmark. He purports that science is so successfully described by mathematics because the physical world is completely mathematical, isomorphic to a mathematical structure, and that we are simply uncovering this bit by bit. In this interpretation, the various approximations that constitute our theories are successful because our mathematical structures provide good approximations of more complex mathematical structures, on which the universe is based. In other words, our successful theories are not mathematics approximating the universe, but mathematics approximating mathematics.
Mathematicians, when working on a problem feel deeply that there is a profound truth out there waiting to be uncovered to solve the problem. Without this hope, they would give up their work. The better mathematicians, it seems, have stronger belief in a solution At the other end of the spectrum, mathematical reasoning itself is used to dismiss the believers. Ironically, when challenged on their belief, their own training betrays mathematicians.
As Sir Arthur Eddington puts it:
“Humans see what they look for. The belief that science is experimentally grounded is only partially true. Rather, our intellectual apparatus is such that much of what we see comes from the glasses we put on.”
The success of mathematics may have more to do with natural selection. We generate a lot of math, and only the good survives. In constructing theories from the observable, the mathematician may not be far off from the paranoid schizophrenic who constructs a logically sounding conspiracy theory from the data presented. (In fact, mathematicians and physicists suffer from the highest incidence of schizophrenia in the population.) Occasionally the paranoia turns out to be based on real conspiracies, and then it is genius.
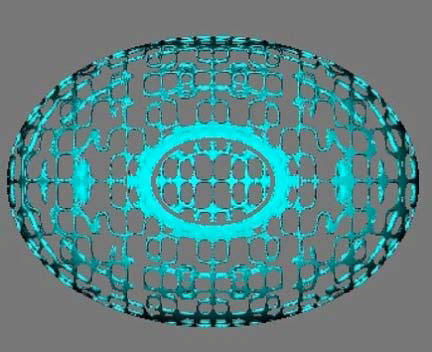
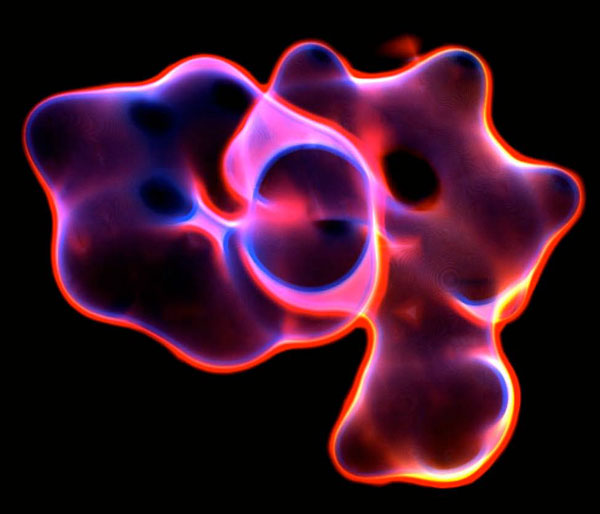
In summary, the mathematician’s relationship with truth is unstable, fluid and malleable, the epitome of a fickle believer. They prefer to talk about validity, or eloquence, or as Poincare put it, “convenience.” They use their belief to drive their craft forward, but fade when challenged to defend it, betrayed by the critical, analytic training that they believe in I conclude this section with a piece of mathematical art, which I call “Ethereal Belief.”
 |
|